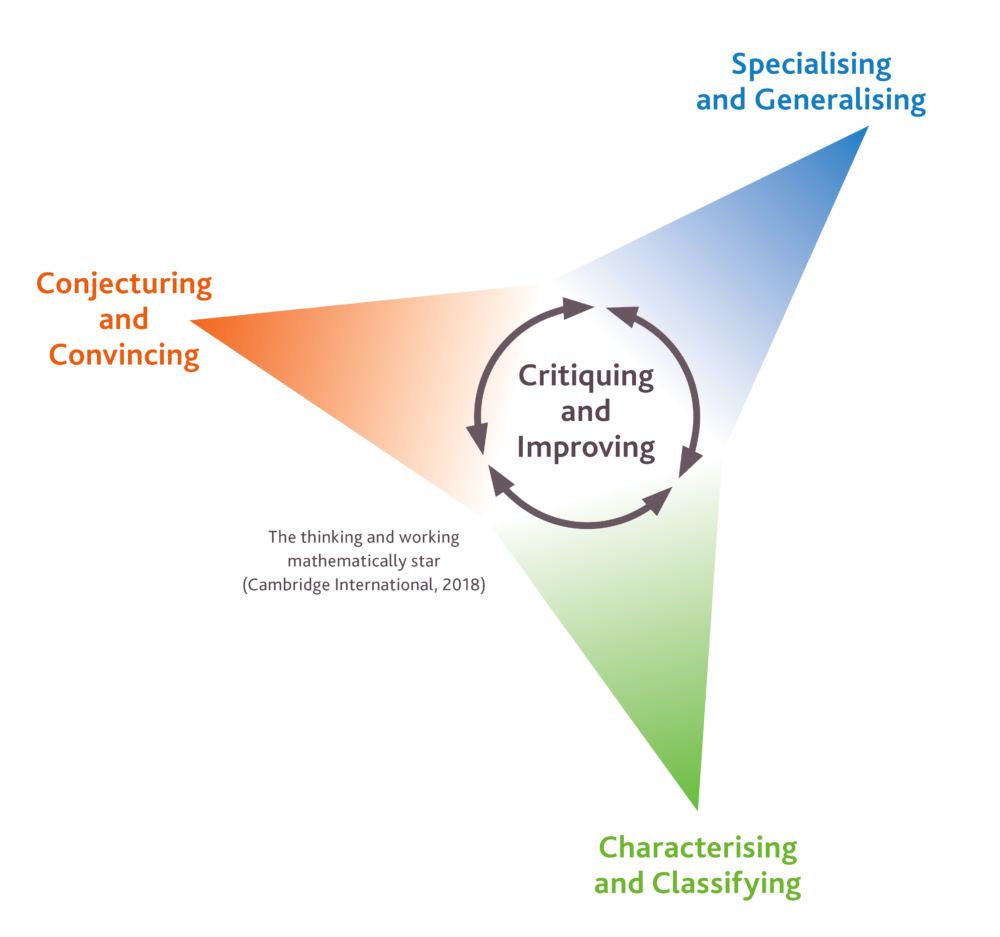
How do you get learners to really think like mathematicians? That question was the starting point for the development of ‘Thinking and Working Mathematically’ (TWM) – one of the most exciting new elements of our improved Cambridge Primary and Lower Secondary Mathematics programme. In this blog I want to explain more about TWM, and why we believe it needs to be a central part of our mathematics curricula.
What is Thinking and Working Mathematically?
Thinking and Working Mathematically (TWM) is a unique feature of our Cambridge Primary and Lower Secondary Mathematics programme. The process of thinking and working mathematically encourages learners to talk with others, challenge ideas and to provide evidence that validates conjectures and solutions. When learners are thinking and working mathematically, they actively seek to make sense of ideas and build connections between different mathematics facts, procedures and concepts. This supports higher order thinking that assists learners in viewing the world in a mathematical way.
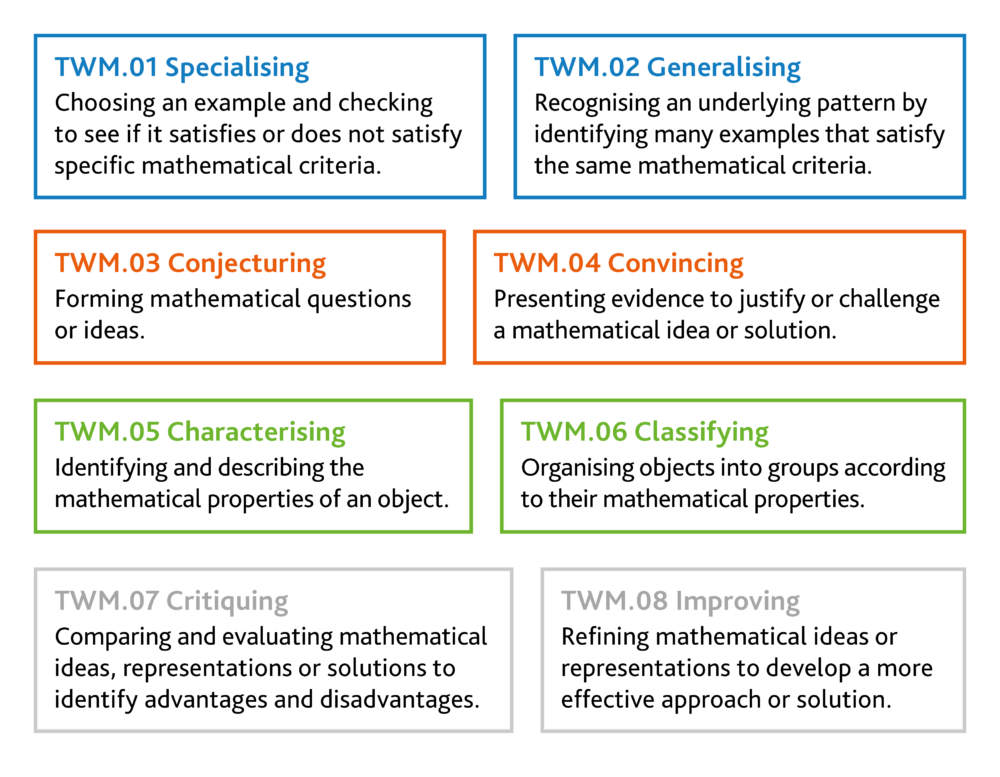
To support teachers and learners in thinking and working mathematically, we have outlined eight TWM characteristics:
Why is Thinking and Working Mathematically important for learners?
When learners are thinking and working mathematically, they actively engage with their learning of mathematics, seeking to make sense of ideas and building connections between different facts, procedures and concepts. Other learners simply follow and carry out processes that they have been shown how to do, without appreciating why they work or what the results mean. Thinking and Working Mathematically can be stimulated by mathematical inconsistencies, patterns or particular representations, and can be improved through practice, reflection and questioning.
What is unique about Thinking and Working Mathematically in the Cambridge Primary and Lower Secondary mathematics programme?
The eight TWM characteristics are:
- embedded throughout the Cambridge mathematics content strands: Number, Geometry and Measure, Statistics and Probability, and Algebra
- the same in Stages 1 to 6 (Primary) and 7 to 9 (Lower Secondary). The teaching and learning activities surrounding the eight characteristics determine the level of complexity of thinking required
- assessed in our Cambridge Progression Tests and Checkpoint and we provide reports for individual learners on their achievement of TWM. These reports highlight the importance of the TWM skills for teachers, parents, and learners
Where did the ideas to enhance problem solving come from?
Up until 2020,problem solving was a separate strand in the Cambridge Primary and Lower Secondary mathematics curriculum. We knew this was problematic as teachers did not appreciate the integrated nature of problem solving because they taught it separately to the other content strands: Number, Geometry, Measure, Data Handling and Algebra.
We wanted to raise the profile of problem solving in our curriculum, our teaching activities, our training, and in our assessments. Although our Progression Tests and Checkpoint assessments in 2016 included problem solving questions, we did not provide reports on these questions that learners answered. So, we were concerned that teachers might not make problem solving a priority.
How did the Cambridge Primary and Lower Secondary Mathematics curriculum design evolve?
We enlisted the help of Cambridge Mathematics (our mathematics research partner) to make sure that the mathematics content was current and based on the latest research. Dr Melise Camargo and I then reviewed the mathematics content to align it to our Cambridge IGCSE and O Level mathematics syllabuses. From this we produced a progression grid from Stages 1 to 9 including an exemplification of each learning objective. You can find this on our primary and lower secondary support sites.
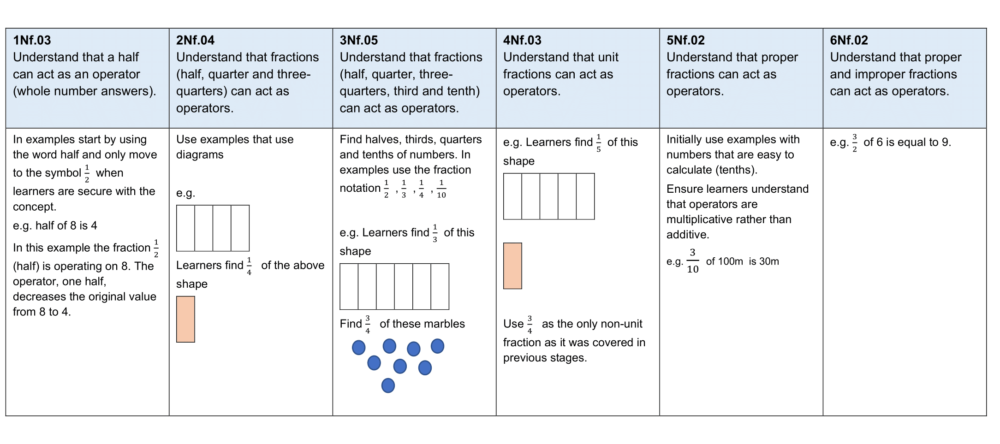
Our next step was to embed Thinking and Working Mathematically into our content strands, making the whole curriculum coherent.
Where did the research come from for Thinking and Working Mathematically?
It was my pleasure to meet Professor John Mason (Oxford University) in person to discuss his book on Thinking Mathematically (1982) as this had inspired my ideas about integrating a version of Thinking Mathematically within our curriculum.
Pólya (1945) and Schoenfeld (1985) have contributed significantly to the debate on problem solving.
‘A problem is a task that the individual wants to achieve, and for which he or she does not have access to a straightforward means of solution’ (Schoenfeld, 1985)
John Mason took these theories and built on them. His research discovered that the skill of generalising, for example, is evident in very young children.
Where can you find examples of Thinking and Working Mathematically activities?
There are some engaging teaching activities in our Cambridge Primary and Lower Secondary Schemes of Work. If you are a registered Cambridge school you can find the Schemes of Work on our primary and lower secondary support sites.

The TWM mathematics characteristics are an exciting and unique feature to the new mathematics curriculum frameworks and our endorsed resources. Our endorsed publishers for our mathematics programme include Thinking and Working Mathematically activities in their resources and also indicate TWM using our star.
Look out for more blogs on Thinking and Working Mathematically teaching activities, and in the meantime, if you are a registered Cambridge school, you can find Thinking and Working Mathematically in the Mathematics section of our support sites: https://primary.cambridgeinternational.org/ and https://lowersecondary.cambridgeinternational.org/ and also on our endorsed partners’ sites:
- Cambridge University Press – go to the CUP hub page
- Collins
- Hodder Education – Hodder Primary and Hodder Lower Secondary
If you are not already registered with us but would like more information about our Primary and Lower Secondary programme, please enter your details here.
Dr Fiona Jackson, Head of Cambridge Primary and Lower Secondary Programme
Many people were involved in the development of Thinking and Working Mathematically within the Cambridge Primary and Lower Secondary mathematics programme. I would like to take this opportunity to thank them for their contributions:
Dr Alison Borthwick, mathematics consultant
Caroline Fawcus, mathematics consultant
Dr Colin Foster, University of Nottingham
Debbie Barton, Lower Secondary Chair, Cambridge International
Professor John Mason, Oxford University
Heather Mahy, Assessment Projects Group, Cambridge International
Jay Surti, Assessment Projects Group, Cambridge International
Lynne McClure, Director, and the Cambridge Mathematics team
Mary Wood, Primary Chair, Cambridge International
Paul Rowbotham, mathematics consultant
Rachel Kerswell, Curriculum Programmes, Cambridge International
Dr Melise Camargo, Curriculum Programmes, Cambridge International
Tim Handley, mathematics consultant
Dr Tim Rowland, University of Cambridge, Faculty of Education
References
Polya. G. (1945) How to Solve it. London: Penguin.
Schoenfeld, A. H. (1985) Mathematical Problem Solving. Orlando, FL: Academic Press.
Mason, J., Burton, L. & Stacey, K. (1982) Thinking Mathematically (revised edition). Harlow: UK: Addison-Wesley Publishers Limited.
Find out more about the improvements to Cambridge Primary and Lower Secondary – www.cambridgeinternational.org/primary-lower-secondary-changes